Jason's chemistry performances have fallen off significantly, and now he has decided to resort to less honorable methods. Jason, being ever clever, devises the perfect strategy to cheat off of Rohan discreetly during his upcoming thermodynamics tests.

The next \(K\) tests have a time limit of \(N\) minutes and will end after \(N\) minutes have elapsed past the start of the test. To avoid raising suspicion, Jason plans to peek at Rohan's test papers at unpredictable intervals. He will peek whenever the number of minutes elapsed is a prime number (only divisible by itself and 1).

However, he also knows that the teacher will leave the classroom for 1 minute every \(M\) minutes, allowing him to peek freely. The teacher leaves the room for the first time after \(M\) minutes have elapsed after the test has began.

Given the number of minutes \(N\) and the interval \(M\), determine the intervals \(t_i\) between the times Jason should peek.

*Note for Python users: submit your solutions in PyPy2 or PyPy3 as the default Python interpreter will time out even with a correct solution.

Constraints

\(1 \le N \le 10^5\)

Subtask 1 [30%]

\(1 \le K \le 10\)

\(N \le M\)

Subtask 2 [70%]

\(1 \le K \le 500\)

\(2 \le M \le 10^2\)

Input Specification

The first line will contain one integer, \(K\). The next \(K\) lines will contain two space separated integer per line. The \(j\)th line contains the time limit for \(N_j\) and the interval \(M_j\) for the \(j\)th test.

Output Specification

Print \(K\) lines where the \(j\)th line contains space separated integers representing the intervals \(t_i\) that Jason will peak at for the \(j\)th test, in chronological order. Do not include the interval between the start of the test and his first peek or the interval between his last peek and the end of the test.

Sample Input

2
20 6
25 5

Sample Output

1 3 3
1 1 2 1 1 1 1 2

Explanation for Sample Output

Jason will peak at minutes \(2,3,5,6,7,11,12,13,17,18,19\). The intervals for this test are therefore \(0,1,0,0,3,0,0,3,0,0\) because each peek lasts for the entire minute. An interval of \(0\) means that Jason continues peeking, so we ignore these. Therefore, the intervals between his peeks are \(1,3\) and \(3\):

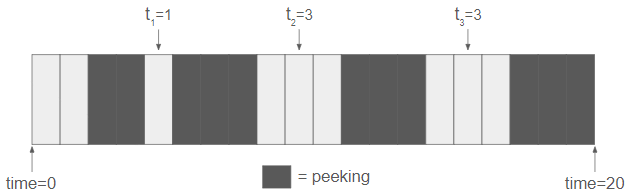
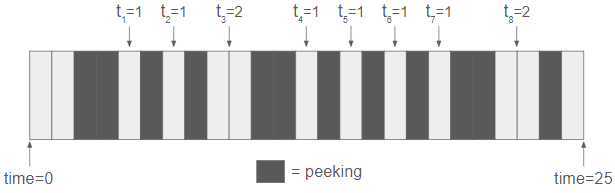
Using similar logic, the intervals which he peeks at for test #2 are as follows: