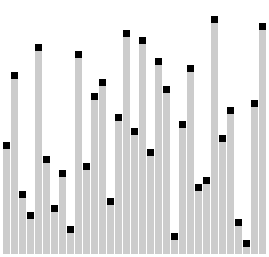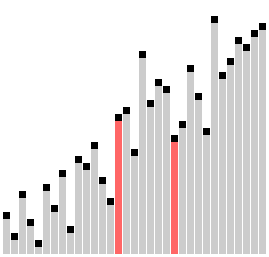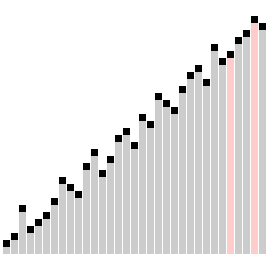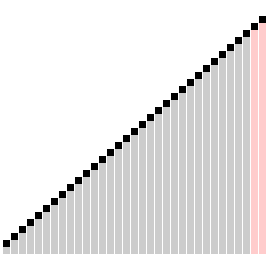
The Comb Sort Algorithm is a variation of the Bubble Sort Algorithm where instead of only comparing adjacent elements, we start by comparing the first and last elements and slowly shrink the gap between the elements we compare. Usually, the rate at which this gap decreases is given as a ratio, but today, we will simply decrease the gap by \(1\) with each loop. For example:

1. On the first loop, compare the \(1^{st}\) and \(n^{th}\) elements and swap if they are out of place.

2. On the second loop, compare the \(1^{st}\) and \(n-1^{th}\) elements, then compare the \(2^{nd}\) and \(n^{th}\) elements, swapping if necessary.

3. On the third loop, compare the \(1^{st}\) and \(n-2^{th}\) elements, then the \(2^{nd}\) and \(n-1^{th}\) elements, and finally the \(3^{rd}\) and \(n^{th}\) elements, swapping if necessary.

This continues until we begin comparing adjacent elements, at which point Comb Sort simply reduces to Bubble Sort.

Given an array of \(N\) integers \(\{a_1, a_2, a_3, ..., a_N\}\), sort the array in non-decreasing order using Comb Sort.

Input Specification

The first line of input will contain \(N\) \((1 \le N \le 200)\).

The second line of input will contain \(N\) space-separated integers, representing each element \(a_i\) \((0 \le a \le 10^6)\) in the array.

Output Specification

On separate lines, output \(N\) space-separated integers representing the final state the array after each swap.

Sample Input 1

9
25 9 11 31 23 2 42 15 26

Sample Output 1

15 9 11 31 23 2 42 25 26
2 9 11 31 23 15 42 25 26
2 9 11 26 23 15 42 25 31
2 9 11 25 23 15 42 26 31
2 9 11 15 23 25 42 26 31
2 9 11 15 23 25 31 26 42
2 9 11 15 23 25 26 31 42

Sample Input 2

1
0

Sample Output 2

No lines of output.